 PDF version of this entire document
PDF version of this entire document
The definitions we have provided for specificity and
generalisation require a measure of separation in image space. The
most straightforward way to measure the distance between images is
to treat each image as a vector formed by concatenating the
pixel/voxel intensity values, then take the Euclidean distance.
This means that each pixel/voxel in one image is compared against
its spatially corresponding pixel/voxel in another image. Although
this has the merit of simplicity, it does not provide a very
well-behaved distance measure since it increases rapidly for quite
small image misalignments [18]. This observation led us to
consider an alternative distance measure, based on the 'shuffle
difference', inspired by the 'shuffle transform' [19].
If we have two images
![]() and
and
![]() , then the shuffle distance
between them is defined as
, then the shuffle distance
between them is defined as
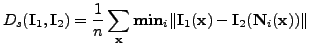 |
(13) |
The idea is illustrated in
Figure 5. Instead of taking the
sum-of-squared-differences between corresponding pixels, the
minimum absolute difference between each pixel in one image and
the values in a neighbourhood around the corresponding
pixel is used. This is less sensitive to small misalignments, and
provides a better-behaved distance measure. The tolerance for
misalignment is dependent on the size of the neighbourhood (![]() ), as is
illustrated in Figure 4.
), as is
illustrated in Figure 4.
|
|
It should be noted that the shuffle distance as defined above depends on the direction in which it is measured (see Figure 6), hence is not a true distance. It is trivial to construct a symmetric shuffle distance, by averaging the distance calculated both ways between a pair of images. However, it was found that the improvement obtained using this was not significant, and did not justify the increased computation time. In what follows, we use the asymmetric shuffle distance.